Sito sulla Scienza di Confine (Frontier Science) "Il vuoto assoluto non esiste!"
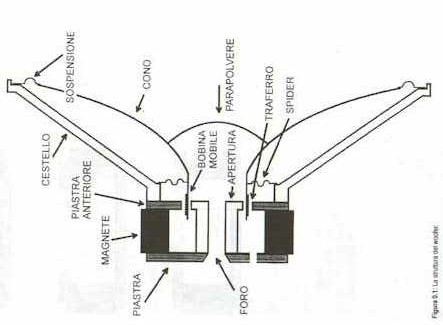
Qualcosa di bizzarro è accaduto all’acqua in Florida dopo il terremoto in Alaska Tratto del link originale : http://theantimedia.org/water-florida-alaska-earthquake/ Poco
Tratto dal link originale : http://daltonsminima.altervista.org/2015/04/15/non-solo-il-98-di-tutti-i-terremoti-soddisfano-la-relazione-lineare-sotto-riportata-ma/ Tutti i terremoti si verificano molto vicino alle ore 06:00 o 18:00 ora locale lunare
Tratto dal link originale : http://daltonsminima.altervista.org/2012/02/20/sole-luna-e-terremoti-1%C2%B0-parte/ Vinayak G. KOLVANKAR Ex scienziato, BARC, 400051 Mumbai, India vkolvankar@yahoo.com Abstract Nel corso di uno
Esistono alcuni fenomeni inusuali che accompagnano i terremoti e di cui non se ne parla molto spesso. Ma che comunque
Premessa : Gran parte degli articoli pubblicati sul Fortunadrago.it necessitano di una conoscenza introduttiva a quella che è nota come
“…Ed invece, come sempre accade per ogni cosa nuova, quando non vilipeso, fui deriso, compassionato e dai più benigni, ritenuto
